يطلب السؤال إيجاد تفاضل او إشتقاق دالة كسرية أو دالة تحتوي على بسط ومقام, في علم التفاضل حينما تواجه مسألة مثل هذا الشكل, دالة كسرية فيجب حينها ان تستخدم قاعدة تسمى "Quotient rule", سوف اختصر لكم هذه القاعدة بأسلوب مبسط عبارة عن خطوات كالآتي:
1 - قم بتسمية قيم البسط جميعها بحرف واحد, لنقل اسمها U, بمعني U تساوي X2 + 3 أو (U = X2 + 3).
2 - قم بتسمية قيم المقام جميعها بحرف واحد, لنقل اسمها V, بمعنى V تساوي X + 1 أو (V = X + 1).
بعد تنفيذ هاتين الخطوتين, لننتقل الآن لتطبيق القاعدة واللتي ستكون كالآتي "باللون الأزرق" (شاهد الصورة):
سنشرح هذه القاعدة بالتفصيل, اطلب منك الآن ان تركز معي:
المقصود بحرف Uَ "ذو علامة فتحة من فوق الحرف" هو إشتقاق او تفاضل U وهي نفس معنى هذا الرمز "du/dx".
بمعنى أن Uَ و du/dx ---> نفس المعنى ---> تفاضل أو إشتقاق U.
اما بالنسبة لما بين القوسين (X) المضروب في كل الحروف الموجودة في البسط, لها عدة معاني, سوف اختصرها لك كالآتي:
Uَ مضروبة في (X) ---> هي نفسها du/dx
V مضروبة في (X) ---> انتبه هنا لن تكون dv/dx, لأن حرف V"من دون علامة فتحة" يعني حرف عادي "لايوجد تفاضل" وبالتالي سوف يكون معناها قيمة المقام كاملة وهي X + 1
Vَ مضروبة في (X) ---> الآن هنا بإمكانك القول ان معناها نفس معنى dv/dx "لان هنالك علامة فتحة على حرف V" بمعنى لابد من عمل اشتقاق لها
وهكذا, هيا بنا الآن لنقسم حل هذا المثال الى خطوات:
- الخطوة الأولى :
اوجد قيمة( U.(x واللتي كما عرفناها انها تساوي قيمة البسط وهي X2 + 3
والآن لنوجد ( Uَ.(x بمعنى تفاضلها , سيكون الجواب كما موضح بالصورة "باللون الأزرق" :
بالنسبة لعملية التفاضل, حينما نشتق او نفاضل X مرفوعة بالأس 2 يكون اشتقاقها كالآتي:
- يجب تنزيل الأس 2 الى جانب X "مضروبة في X" ولكن بشرط: يجب طرح 1 من قيمة الأس "2" بمعنى حتى يستطيع الرقم 2 ان ينزل الى جانب X لابد من طرحه من 1 (2 - 1 = 1) وبتالي نستطيع تنزيل 2 ويصبح الأس بعد الطرح يساوي 1
اذن الجواب : 2X كما تشاهد لايوجد رقم مكتوب فوق حرف X لأن الأس يساوي 1"عادة الرقم 1 لا يكتب"
اما بالنسبة لإشتقاق الرقم 3, في علم التفاضل اشتقاق او تفاضل أي رقم يساوي 0, وبالتالي اشتقاق الرقم 3 يساوي 0
اذن الجواب النهائي بالنسبة ( Uَ.(x تساوي 2X, وهكذا انتهينا من الخطوة الأولى من الحل.
- الخطوة الثانية:
نوجد قيمة ( V.(x واللتي كما عرفناها تساوي قيمة المقام كاملة وهي X + 1
والآن لنوجد ( Vَ.(x واللتي تعرف على انها اشتقاق V وبالتالي اشتقاقها او تفاضلها كما موضح في الصورة :
بالنسبة للتفاضل, اولا سوف نشتق X, وكما هو موضح أن درجة القوى او الأس بالنسبة لــX يساوي 1 , وبالتالي حين اجراء عملية التفاضل لابد من تنزيل الأس 1 الى جانب X بحيث تكون مضروبة في X ولكن بشرط: ان يتم طرح 1 من الأس قبل ان يتم التنزيل , بمعنى يجب طرح 1 من الأس 1 حتى يتم التنزيل, وبالتالي (1 - 1 = 0), اذن اصبحت قيمة الأس بالنسبة لــX الآن تساوي 0 , في علم التفاضل اذا كانت درجة الأس بالنسبة للمجاهيل مثل X تساوي 0 ذلك يعني ان القيمة الكلية لها تساوي 1, بمعنى:
X مرفوعة بالأس 0 = 1, وبالتالي اصبح لدينا الرقم 1 الخاص بالأس بعد ماتم تنزيله مضروب في قيمة X المرفوعة بالأس 0 واللتي تساوي واحد , اي ان 1 مضروب في 1 وبالتالي تساوي 1
اذن إشتقاق X يساوي 1.
بعد ما تم اشتقاق X, لننتقل لإشتقاق الرقم 1 , وكما قلنا سابقا إشتقاق اي رقم يساوي 0, وبالتالي إشتقاق 1 يساوي 0.
اذن الجواب النهائي لقيمة ( Vَ.(x تساوي 1 "كما موضح في الصورة اعلاه عند الخطوة الثانية".
- الخطوة الثالثة:
إيجاد التربيع لقيمة ( V.(x, كل ماعليك هو ان تضع قيمة المقام كاملة بين قوسين مرفوعة بالأس 2 "كما موضح في الصورة أعلاه عند الخطوة الثالثة".
- الخطوة الرابعة:
والآن بعد ان اوجدنا كل العناصر المطلوبة, لنكتب القاعدة كاملة واللتي ستكون الحل لهذا المثال "شاهد الصورة عند الخطوة الرابعة":
كل ما عليك في الخطوة الرابعة هو فقط كتابة القاعدة بعد تعويض العناصر اللتي اوجدناها في الخطوات السابقة لتتحصل على اجابة هذا المثال, كما بإمكانك تبسيطها بشكل اكثر اذا اتممت عملية الضرب الموجودة في البسط.
وهكذا انتهينا من حل المثال الذي تعلمنا من خلاله على كيفية التعامل مع الدوال الكسرية وكيفية إشتقاقها او تفاضلها واللتي تتم عن طريقة تطبيق قاعدة "Quotient rule".





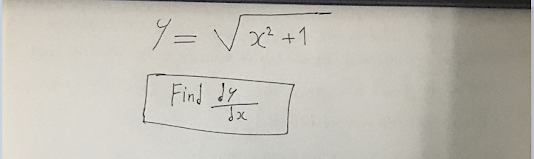

تعليقات
إرسال تعليق