في مادة المعادلات التفاضلية, سوف تدرس نوعين رئيسيين من المعادلات وهما:
- معادلة تفاضلية عادية "Ordinary differential equations"
- معادلة تفاضلية جزئية "Partial differential equations"
ولكن السؤال الأهم, ماهو الفرق بين المعادلتين؟
سنوضح الفرق بين المعادلتين من خلال هذا المثال الموجود في الصورة أعلاه, يكمن الفرق بين المعادلتين في عدد المشتقات داخل المعادلة , فعلى سبيل المثال اذا كانت هنالك معادلة كالآتي:
dA/dn + 2 = 0
والآن قبل ان نحدد كم عدد المشتقات, لابد ان نفرق اولاً بين العنصر الذي سيطبق عليه الإشتقاق او التفاضل وبين العنصر العادي, والآن ركز على العنصر المتواجد في البسط والذي يحتوي على dA , هذا العنصر يعتبر عنصر عادي بمعنى انه لن يتم اجراء عملية الإشتقاق او التفاضل عليه, من هو العنصر الذي سوف يجرى عليه عملية الإشتقاق؟
هو العنصر المتواجد في المقام وهو dn, هذا العنصر هو الذي سوف يجرى عليه عملية الإشتقاق لأنه متواجد في المقام.
متواجد في المقام؟ هل هذا كافي لنفهم المعلومة كاملة؟, لنوضح اكثر ماذا يعني ان يكون العنصر متواجد في المقام؟
dA/dn ---> تعني ان المعادلة بإسم A, وان الإشتقاق سيتم للمتغير n, كيف عرفنا ذلك؟ من خلال تحديد العنصر الموجود في البسط والمقام.
اذن طالما اننا نمتلك مجهول واحد سيجرى عليه الإشتقاق هذا يعني ان هذه المعادلة تسمى معادلة عادية"Ordinary differential equations",بسبب ان عملية الإشتقاق ستجرى لعنصر واحد فقط.
والآن اذا المثال يحتوي على اكثر من عنصر يجرى عليه الإشتقاق هل سيتغير نوع المعادلة؟
نعم سوف تصبح معادلة تفاضلية جزئية "Partial differential equations"
الفرق يكمن في العناصر اللتي سيجرى عليها الإشتقاق, اذا كانت واحدة تسمى معادلة تفاضلية عادية واذا كانت اكثر من ذلك تسمى معادلة تفاضلية جزئية.
والآن شاهد الصورة:
لاحظ انه في الفقرة الأولى, يوجد عنصر واحد فقط سيجرى عليه الإشتقاق وهو العنصر X, لماذا X تحديداً؟ لأنه موجود في المقام او بإمكانك القول بصيغة اخرى ان y يعتبر عنصر عادي بحكم وجوده في البسط ولكن X موجود في المقام وبالتالي عملية التفاضل ستجرى على المتغير X وطالما ان X هو المتغير الوحيد الموجود في المقام, اذن هذه المعادلة هي معادلة عادية.
اما بالنسبة للفقرة الثانية "b", لاحظ ان هنالك اكثر من عنصر موجود في المقام X و Z, وبالتالي هنالك اكثر من عنصر واحد سيجرى عليه الإشتقاق, طالما انه اكثر من عنصر واحد, اذن هذه المعادلة تسمى معادلة تفاضلية جزئية "Partial differential equations".
اذن الجواب النهائي لهذا المثال سيكون كالآتي:
- الفقرة الأولى "a", نوع المعادلة التفاضلية هي معادلة عادية لأنها تحتوي على عنصر واحد سيجرى عليه عملية الإشتقاق.
- الفقرة الثانية "b", نوع المعادلة التفاضلية هي معادلة جزئية لأنها تحتوي على اكثر من عنصر واحد سيجرى عليه عملية الإشتقاق.
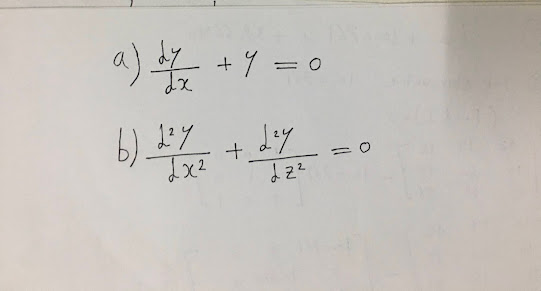
تعليقات
إرسال تعليق