أساسيات تحديد المعادلات الخطية من المعادلات التفاضلية (شرح كامل على كافة الخطوات)

 تحديد المعادلات الخطية من المعادلات التفاضلية

سنتعلم في هذا الدرس حول الأساسيات في تحديد المعادلات الخطية (تعرف بالإنجليزية Linear equation) من المعادلات التفاضلية, ولتحديد ذلك يجب ان نتعلم أولا عن العناصر التابعة والعناصر المستقلة اللتي تكون موجودة في المعادلة التفاضلية, ولكن ماهي العناصر التابعة وماهي العناصر المستقلة؟

الجواب: العناصر التابعة (تعرف بالإنجليزية dependent variable): هي العناصر اللتي لايجرى عليها عملية الإشتقاق, فعلى سبيل المثال :

y = x + 1

افرض انني قلت لك اوجد إشتقاق هذه المعادلة بصيغة dy/dx, والآن من هو العنصر التابع هنا او من هو العنصر الذي يطلق عليه dependent variable؟

الجواب: y, لأن من خلال الصيغة dy/dx, لوحظ ان رمز dy موجود في البسط وهذا معناه ان الإشتقاق سيكون بالنسبة لــ X فقط, لانستطيع تفاضل y, ولكن سنفاضل المتغير x لأن x موجودة في المقام

اذن نستطيع الآن إستنتاج أن العنصر التابع هو العنصر الذي لا يجرى عليه عملية التفاضل او الإشتقاق

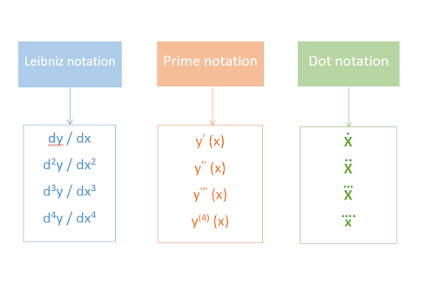
ملحوظة: يجب أن لاتنسى ان هنالك ثلاث انواع من رموز التفاضل, بمعنى ليس شرطا ان اقول لك اوجد تفاضل dy/dx, استطيع ان اقول لك اوجد التفاضل بصيغة اخرى ولكن المعنى واحد, ارفقت لك الصورة التالية حول صيغ التفاضل الثلاث مع الأمثلة:

والآن بعد شرح مفهوم العنصر التابع, لننتقل الى التالي:

العناصر المستقلة (تعرف بالإنجليزية Independent variables), وهي العناصر اللتي يجرى عليها عملية التفاضل او الإشتقاق, على سبيل المثال:

y = x + 1

حينما اقول لك اوجد dy/dx, ستوجد التفاضل او الإشتقاق بالنسبة للمتغير من؟

الجواب: x, بمعنى سنفاضل x او بصيغة اخرى سنفاضل محتوى العنصر التابع"y" بالنسبة للمتغير x, لأن x موجودة في المقام من صيغة dy/dx

اذن نستطيع الإستنتاج أن العناصر المستقلة او Independent variables هي العناصر اللتي يجرى عليها عملية الإشتقاق او التفاضل.

والآن لننتقل إلى درسنا لهذا اليوم وهو كيفية تحديد المعادلات الخطية من المعادلات التفاضلية, هنالك ثلاث نقاط أساسية يجب معرفتها لتحديد المعادلة التفاضلية من حيث كونها خطية ام لا, وهي كالتالي:

1 - العناصر التابعة dependent variables ومشتقاتها "بمعنى درجات تفاضلها" يجب ان يكونوا جميعهم مرفوعين بالأس واحد"1", شاهد الصورة التالية :

من هو العنصر الذي يطلق عليه dependent variable من خلال الصورة أعلاه؟

الجواب: y, صيغة التفاضل اللتي ظهرت في هذه الصورة هي من نوع Prime notation, والآن لنركز على هذه المعادلة ونحدد هل هي معادلة خطية ام لا بتطبيق النقطة رقم 1

لاحظ ان عناصر الــ dependent كلها مرفوعة بالأس 1, العنصر الأول y "من جهة اليسار" مرفوع بالأس 1 ودرجة إشتقاقه 2 ( انتبه درجة الإشتقاق ليس معناه قيمة الأس,حيث قيمة الأس هنا تساوي 1) , انظر للعنصر الآخر من y لاحظ ان درجة إشتقاقه 1 مرفوع بالأس 1, ومن ثم بعد إشارة الزائد "+" هنالك عنصر آخر من y لايحتوي على درجة إشتقاق ولكن قيمة الأس تساوي 1, اما العنصر الآخر "مابعد اشارة =" يحتوي على  e مرفوع بالأس x سوف نتجاهل هذا العنصر الآن لأننا نشرح فقط النقطة رقم 1 لتوضيح مفهومها وسنتطرق لهذا العنصر في النقطتين التاليتين, اذن من خلال قراءة هذه المعادلة استنتجنا ان جميع عناصر الــ dependent مرفوعة بالأس 1, اذن نقطة رقم 1 تحققت, وبالتالي هذه المعادلة هي معادلة خطية "Linear equation".

والآن لننتقل الى مثال آخر حول النقطة رقم 1, شاهد الصورة التالية:

لاحظ ان هذا المثال مشابه للمثال الأول, ولكن ركز على العنصر الثالث من y الموجود بعد إشارة الزائد"+", نلاحظ ان هنالك عنصر من الـــ dependent مرفوع بالأس 2, وبالتالي هذه المعادلة غير متوافقة مع النقطة رقم 1, اذن هذه المعادلة التفاضلية غير خطية"non linear equation".

مثال آخر حول النقطة رقم 1, شاهد الصورة التالية:

لاحظ في هذا المثال المشابه ايضا للمثال الأول, العنصر الثاني من y بعد إشارة الطرح "-" درجة إشتقاقها واحد ولكن مرفوعة بالأس كم؟, مرفوعة بالأس 4, وهذا مخالف للنقطة رقم 1 حيث تنص النقطة انه لابد ان يكون جميع عناصر الــ dependent  مرفوعين بالأس 1, اذن هذه المعادلة التفاضلية هي معادلة غير خطية "non linear equation"

والآن بعد توضيح المفهوم من النقطة رقم 1, لننتقل الآن إلى النقطة الثانية:

2 - يجب ان لاتكون العناصر التابعة dependent داخلة في أي شكل من أشكال الدوال:

شاهد الصورة التالية :

لاحظ في هذا المثال المشابه للمثال الأول, ركز على العنصر e الموجود بعد إشارة "=" نلاحظ ان هذه الدالة على ماذا احتوت؟ لقد احتوت على العنصر dependent وهو العنصر y حيث انها مرفوعة بالأس y وهذا لايتوافق مع النقطة رقم 2 واللتي تنص على ان جميع عناصر الــ dependent يجب ان لاتكون داخلة في اي دوال سواء دالة مثل e او اي دالة اخرى, وبالتالي هذه المعادلة التفاضلية معادلة غير خطية "non linear equation".

3 - يجب ان لاتحتوي المعادلة التفاضلية على عناصر تابعة dependent ومشتقاتها بحيث تكون "مضروبة" في بعض

شاهد الصورة التالية:

لاحظ في هذا المثال, يوجد عناصر dependent وهي y مضروبة في بعض وهذا لايتوافق مع النقطة رقم 3, هل هنالك ملاحظة اخرى؟ نعم بالنسبة لنقطة رقم 2 واللتي تنص على انه يجب ان لاتكون العناصر التابعة dependent داخلة في أي شكل من أشكال الدوال, حيث نلاحظ ان الدالة e مرفوعة بالأس y وهذا غير متوافق مع النقطة رقم 2, وبالتالي هذه المعادلة التفاضلية هي معادلة غير خطية "non linear equation".

هذه هي النقاط الثلاث الأساسية لتحديد المعادلات الخطية من المعادلات التفاضلية, تذكرها دوما وقم بمراجعتها لأنك بحاجة إليها خصوصا في المواد المتعلقة بالمعادلات التفاضلية.