سنركز في درسنا لهذا اليوم عن الأساسيات في تحليل القوى العادية والقوى الموزعة بإنتظام بشكل متساوي والقوى الموزعة بإنتظام على شكل مثلث بإستخدام المومنت, هدفنا من خلال هذا الدرس هو تقوية أساسياتك في تحليل القوى بأنواع مختلفة, سوف نقدم لك ثلاثة أمثلة على حدى, المثال الأول سيكون عن القوى العادية , والثاني سيكون على القوى الموزعة بإنتظام بشكل متساوي, والمثال الثالث سيكون عن القوى الموزعة بإنتظام على شكل مثلث, هيا بنا لنبدأ:
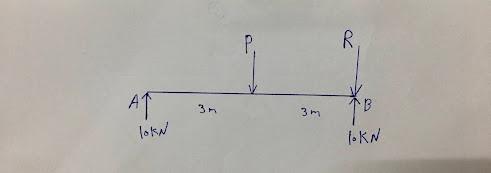
كما نلاحظ في هذا المثال, تحتوي العارضة "Beam" على قوى معلومة وقوى مجهولة, حيث ان هنالك قوتين تساوي 10kN على طرفي العارضة, كما ان هنالك قوى في منتصف العارضة وفي الطرف الأيمن ايضا وهما قوى مجهولة P,R
المطلوب هو ان نوجد مقدار هاتين القوتين
لنبدأ الآن بالخطوة الأولى وهو استخدام معادلة القوى على محور y بحكم ان جميع القوى على العارضة قوى عمودية وبالتالي سنتعامل مع محور y فقط , شاهد الصورة التالية:
بعد استخدام قوانين تحليل القوى بأخد جميع القوى على محور y مع الإفتراض ان القوى المتجهة للأعلى بالسهم تكون قوى موجبة, تحصلنا على هذا الناتج كما هو موضح في الصورة أعلاه, لاحظ ان في البداية الرقمين 10 إشارتهم موجبة لأن كلا القوتين في العارضة متجهة للأعلى وبالتالي إشارتهم موجبة, ولكن لاحظ للقوتين P,R حيث ان إشارتهم سالبة لأن كلا القوتين متجهتين للأسفل على العارضة وبالتالي تصبح إشارتهم سالبة, اذن بعد الحساب كما هو موضح في الصورة أعلاه ظهر لدينا قوتين مجهولتين, بمعنى لم نستطع إيجاد قيمة القوتين المجهولتين او احدهما بإستخدام معادلة تحليل القوى على y, وبالتالي يلزم علينا الإنتقال الى خطوة اخرى لإيجاد قيمة احد القوى المجهولة لتعويضها في هذه المعادلة, ولكن ماهي الخطوة الثانية؟
الجواب: ستكون الخطوة الثانية بإستخدام المومنت واللتي ستمكننا من حل احد القوتين المجهولتين, شاهد الصورة التالية:
لاحظ في الصورة أعلاه في الخطوة الثانية, لقد استخدمنا معادلة المومنت مع الإفتراض ان اي قوى تكون متجهة عكس عقارب الساعه ستكون قوى موجبة وعكس ذلك ستكون قوى سالبة, كما اننا اخذنا المومنت عند النقطة B, لماذا؟
الجواب: لأنه حينما تأخذ المومنت في نقطة معينة وتكون هذه النقطة يقع عليها قوى او اكثر من قوى سوف تتجاهلها في معادلة المومنت, واي قوى تكون موجهة إلى النقطة اللتي اخذت منها المومنت سوف تتجاهلها ايضا,حسننا اذا افترضنا اننا اخذنا المومنت عند النقطة A ماهي المشكلة اللتي سوف تواجهنا؟
الجواب: حينما تأخذ المومنت عند النقطة A سوف تتجاهل القوى الواقعه على نفس النقطة, حسب ماهو موضح في العارضة هذه القوى اللتي سوف تتجاهلها هي 10kN, هل هنالك قوى أخرى سوف تتجاهلها؟
الجواب: لا, اذن حينما تكتب معادلة المومنت سيظهر لك في النهاية قوتين مجهولتين وبالتالي لم تستفد شيئا من اخذ المومنت عند النقطة A
وبالتالي القرار الصائب هو ان تأخذ المومنت عند النقطة B, لاحظ في الصورة أعلاه حينما نأخذ المومنت عند النقطة B سوف نتجاهل القوى R بالإضافة الى القوى 10kN, لايهمنا تجاهل القوى المعلومة 10 بقدر ما يهمنا هو تجاهل القوى المجهولة حتى نستطيع إيجاد قيمة احد القوتين المجهولتين, على اي حال, سوف تتجاهل القوتين المعلومة والمجهولة لأنها تقع بنفس النقطة اللتي اخذت منها المومنت وهي النقطة B , والآن لاحظ في الصورة في الخطوة الثانية, لاحظ اننا كتبنا القوى 10 بإشارة سالبة, لماذا؟
الجواب: لأنها متجهة مع عقارب الساعه بالنسبة للنقطة B, اذن اشارتها سالبة, لاحظ اننا ضربنا هذه القوى في 6 لأن النقطة اللتي اخذنا منها المومنت هي النقطة B والقوى 10 واقعه عند النقطة A, وبالتالي مسافتها الى النقطة B تساوي 6m, اذن لابد من ضربها في القوى 10, (لاحظ الفرق بين معادلتي y اللتي في الخطوة الأولى ومعادلة المومنت في الخطوة الثانية, الفرق هو انك سوف تستخدم القوى العادية في معادلة y بدون ضربها في المسافة, ولكن في المومنت يجب ضرب القوى في المسافة), لاحظ في الصورة أعلاه اننا استخدمنا القوى P في معادلة المومنت بإشارة موجبة لماذا؟ لأنها متجهة عكس عقارب الساعه بالنسبة للنقطة B وبالتالي يجب ان تكون إشارتها موجبة وتكون مضروبة في المسافة 3 لأن المسافة بين القوى المجهولة P والنقطة اللتي اخذنا منها المومنت B تساوي 3m, وبعد الحساب ظهر لدينا قوى مجهولة واحدة واصبح بإمكاننا إيجاد قيمتها واللتي تساوي حسب ما هو موضح في الصورة أعلاه ان القوى P تساوي 20kN, والآن لنكمل خطوات الحل, شاهد الصورة التالية:

لاحظ في الصورة أعلاه, بعد إيجاد القوى المجهولة P واللتي تساوي 20kN سنقوم بتعويضها في معادلة y لإيجاد قيمة القوى R, وكما هو موضح في الصورة أعلاه, بعد الحساب تبين ان قيمة القوى R تساوي 0.
لننتقل الآن إلى المثال الثاني الذي يحتوي على قوى موزعة بإنتظام بشكل متساوي, شاهد الصورة التالية:
لاحظ في هذا المثال, انه مشابه للمثال السابق, في الحقيقة كل الأمثلة متشابهه لأننا نريد منك أن تتعلم وان تعرف الفرق بين المثال الأول والثاني والثالث وهذا هو هدفنا, والآن لنبدأ بحل هذا المثال, المطلوب إيجاد القوتين المجهولة P,R ولكن لاحظ الفرق أن شكل القوى P تغيرت عن السابق, وهذا هو الفرق بين القوى العادية والقوى الموزعة بإنتظام بشكل متساوي, والآن لنبدأ بكتابة اولى خطوات الحل وهو كتابة معادلة تحليل القوى على محور y لأن جميع القوى على العارضة قوى عمودية, شاهد الصورة التالية:

لاحظ في الصورة أعلاه, اخذنا جميع القوى العمودية على العارضة , حيث ان القوتين المعلومتين 10kN اشارتهم موجبة في المعادلة لأنهم متجهين للأعلى, ولكن القوى R إشارتها سالبة لأنها متجهة للأسفل, والآن لاحظ بالنسبة للقوى P إشارتها سالبة لأنها متجهة للأسفل لكن لاحظ الفرق اننا ضربناها في 3 رغم انه في المثال الأول وفي معادلة y لم نضرب اي قوى في المسافة, فلماذا الآن ضربنا القوى P في المسافة 3m؟
الجواب: لأن القوى P مختلفة عن اي قوى موجودة في العارضة في هذا المثال ومختلفة عن اي قوى موجودة في العارضة في المثال السابق, حيث ان القوى P في هذا المثال هي قوى موزعة بإنتظام بشكل متساوي ولكن القوى الأخرى هي قوى عادية, وبالتالي القوى الموزعة بإنتظام يجب ان تضرب في المسافة ولكن اي مسافة؟
الجواب: يتم ضربها في المسافة اللتي تؤثر القوى عليها على العارضة, لاحظ بداية القوى P من النقطة A ونهايتها عند منتصف العارضة, كم هذه المسافة؟ تساوي 3 وبالتالي طالما انها قوى موزعة بإنتظام اذن يجب ضربها في 3, والآن بعد الحساب ظهر لدينا كما هو موضح في الصورة أعلاه قوتين مجهولتين وبالتالي سنتوقف مؤقتا وننتقل الآن الى الخطوة الثانية بإستخدام المومنت
سوف نأخذ المومنت عند النقطة B حتى نستطيع تجاهل القوى المجهولة R وهذا المهم, ولكن يجب ان لاننسى ايضا اننا سوف نتجاهل القوى 10 لأنها ايضا واقعه على النقطة B, شاهد الصورة التالية:
لاحظ في الصورة أعلاه في الخطوة الثانية, إشارة القوى 10 سالبة لأنها متجهة مع عقارب الساعه بالنسبة للنقطة B وبالتالي إشارتها سالبة ومضروبة في المسافة 6, ولكن لاحظ بالنسبة للقوى P سوف يختلف التعامل معها لأن P قوى موزعة بإنتظام بشكل متساوي وبالتالي هنالك خطوتين يجب معرفتهما:
1- كتابة القوى P مع الإنتباه للإشارة اذا سالبة او موجبة, حسب ماهو موضح الآن الإشارة موجبة لأنها متجهة عكس عقارب الساعه بالنسبة للنقطة B
2 - ضربها في المسافة 3m, هذه المسافة ليست المسافة مابين القوى P الى النقطة B, لا هذه مسافة P كاملة على العارضة, لاحظ ان القوى P بدأت من النقطة A وانتهت عند منتصف العارضة, وبالتالي المسافة 3m, اذن نضرب 3 في P
3- ضربها في المسافة بين النقطة اللتي اخذت منها المومنت إلى منتصف مسافة تأثير القوى P على العارضة , الآن نحن قلنا سابقا ان مسافة تأثير القوى P هي 3m او بصيغة بأخرى مسافة تأثير القوى P معناه بداية القوى P ونهايتها اللتي تنتهي بمنتصف العارضة, جيد والآن منتصف تأثير القوى P على العارضة يعني سوف نقسم 3 على 2 لأننا نريد النصف, اذن تساوي 1.5, لاحظ هذا النصف فقط, والآن سوف نحسب من هذا النصف الى النقطة B , وباتالي 1.5 + 3 = 4.5m, اذن سوف نضربها في 4.5
يجب ان لاتنسى تلك الخطوات السابقة فهي مهمة جدا وتختلف بينها وبين القوى العادية, حيث ان القوى العادية نضربها في المسافة مباشرة ولكن بالنسبة للقوى الموزعة بإنتظام يختلف التعامل هنا ولابد من الإلتزام بتلك الخطوات الثلاث, والآن بعد الحساب ظهر لدينا قوى مجهولة واحدة كما هو موضح في الصورة أعلاه حيث ان نتيجة P تساوي 4.44kN
والآن لنعود الى معادلة y بتعويض القيمة P لإيجاد القوى المجهولة R, شاهد الصورة التالية:
كما هو موضح في الصورة أعلاه, كل ماعليك هو تعويض القيمة P في المعادلة لإيجاد القوى المجهولة R واللتي تساوي بعد الحساب 6.66kN
لننتقل الآن إلى المثال الثالث والذي يحتوي على قوى موزعة بإنتظام على شكل مثلث, شاهد الصورة التالية:

لاحظ هنا ان القوى P اختلفت عن المثال الأول والثاني, حيث ان في المثال الأول كانت القوى P مثل بقية القوى على العارضة قوى عادية, وفي المثال الثاني كانت القوى P مختلفة بحيث انها قوى موزعة بإنتظام بشكل متساوي, والآن في هذا المثال الثالث اختلفت القوى P بحيث انها قوى موزعة بإنتظام على شكل مثلث, والآن لنبدأ بحل هذا المثال حيث ان المطلوب هو إيجاد القوتين المجهولتين P,R, لنبدأ الآن بأولى الخطوات وهي كتابة معادلة تحليل القوى y, شاهد الصورة التالية:
لاحظ هنا أن القوتين 10kN موجبة لأنها متجهة للأعلى, ولكن لاحظ للقوى P إشارتها سالبة لأنها متجهة للاسفل ولكن لاحظ لأنها قوى موزعة بإنتظام على شكل مثلث فلابد من تطبيق قاعدة واللتي تنص على الآتي:
الطول في العارض في الإرتفاع ---> قاعدة المثلث العامة
وبالتالي نصف مضروبة القاعدة واللتي تساوي 3m حيث انها بداية المثلث ونهايته مضروبة في الإرتفاع واللتي هي القوى المجهولة P (انتبه هذه القاعدة خاصة بالقوى الموزعة بإنتظام على شكل مثلث), والآن بعد الحساب ظهر لدينا قوتين مجهولتين,اذن سنتوقف مؤقتا وسننتقل لإيجاد احد القوى المجهولة بإستخدام المومنت عند النقطة B, شاهد الصورة التالية:
كما هو موضح في الصورة أعلاه عند الخطوة الثانية, لاحظ ان إشارة القوى 10 سالبة لأنها متجهة مع عقارب الساعه بالنسبة للنقطة B مضروبة في المسافة واللتي تساوي 6m وهي المسافة بين القوى والنقطة B, اما بالنسبة للقوى P فهي موجبة لأنها متجهة عكس عقارب الساعه بالنسبة للنقطة B, ولكن لأنها قوى موزعة بإنتظام على شكل مثلث فلا يمكن كتابة القوى P بمفردها, يجب كتابة قانون المثلث كما طبقنا ذلك في المعادلة y , القاعدة تنص على:
نصف في القاعدة في الإرتفاع,بحيث نصف مضروبة في 3 مضروبة في الإرتفاع P
ولكن الآن هذه القاعدة كلها عبارة عن قوى, مازلنا لم نضرب في المسافة بعد, وكما تعلم في المومنت يجب ان نضرب في المسافة بين القوى الى النقطة B, ولكن هنالك خطوات خاصة للقوى الموزعة بإنتظام على شكل مثلث تختلف عن القوى العادية والقوى الموزعة بإنتظام بشكل متساوي, الخطوات كالآتي:
1- ضربها في 2/3 مضروب في 3, بمعنى ضرب قاعدة المثلث في "ثلثي"المسافة P المؤثرة على العارضة, ثلثي معناها 2/3 ومسافة P المؤثرة على العارضة كما نعلم تساوي 3m , ولكن لماذا قلنا ثلثي المسافة ولم نقل ثلث المسافة؟
الجواب: النقطة اللتي اخذنا منها المومنت وهي النقطة B تقع على يمين المثلث صحيح؟, ممتاز, ركز على نهاية شكل المثلث, يبدأ من منتصف العارضة ولكن نهايته عند النقطة A صحيح؟, ممتاز, والآن ركز في الصورة التالية:

لاحظ في هذه الصورة نريد التوضيح لك بخصوص هذه النقطة الهامة وهي تحديد المسافة الخاصة بالقوى الموزعة بإنتظام على شكل مثلث واللتي سوف نقوم بضربها في قاعدة المثلث, أولا حينما نقول ثلثي او ثلث المسافة, المقصود به هو علامة X الموجودة في الصورة باللون الأخضر, الآن هذا الرمز X يمثل ثلث مسافة المثلث ولكن السؤال الآن في اي نقطة اخذت المومنت؟ الجواب هو عند النقطة B صحيح؟ ممتاز , اذن سوف تأخذ المسافة على يمين الرمز X وبالتالي سوف تأخذ المسافة 2/3 مضروبه في 3 , بمعني ثلثي المثلث مضروب في مسافة تأثير P على العارضة واللتي تساوي 3, (افرض انك اخذت المومنت عند A, هنا سوف تأخذ ثلث المسافة بمعنى 1/3 مضروب في 3, انتبه لهذه النقطة جيدا), والآن لاحظ لم ننتهي بعد, ثلثي المثلث المضروب في 3 هو فقط المسافة ما بين رمز X الى منتصف العارضة كما هو موضح باللون الأخضر, ولكن انت بحاجة المسافة الكلية الى النقطة B, اذن سوف تجمع 2/3 مضروب في 3 زائد المسافة 3 وبالتالي هذه المسافة ستضربها في قاعدة المثالث, شاهد الصورة التالية:

بعد شرح النقطة الهامة المختصة بمسافة القوى الموزعة بإنتظام على شكل مثلث واللتي سنضربها في قاعدة المثلث, سنواصل كتابة معادلة المومنت وحساب القوى المجهولة P واللتي تساوي 8kN, ثم بعد ذلك نعود إلى معادلة y بتعويض القيمة P لإيجاد القوى المجهولة R, واللتي اصبحت قيمتها بعد الحساب تساوي 8kN.
انتهى درسنا لهذا اليوم, هدفنا من خلال هذا الدرس هو تقوية اساسياتك في تحليل القوى والتعامل مع انواع مختلفة من القوى المؤثرة كالقوى العادية والقوى الموزعة بإنتظام بشكل متساوي والقوى الموزعة بإنتظام على شكل مثلث, قم بمراجعة الدرس مرات عديدة بالقراءة والكتابة لتعزيز وتقوية اساسياتك في تحليل القوى.














تعليقات
إرسال تعليق