تدريب على إيجاد مسافة القوى الموزعة بإنتظام على شكل مثلث بإستخدام المومنت

 

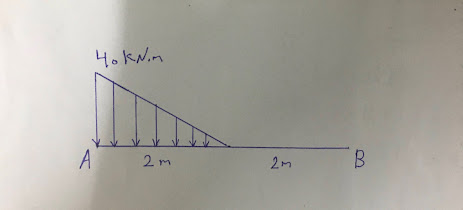
في هذا المثال سوف نركز بشكل كبير على نقطة هامة جدا وهي كيفية إستنتاج المسافة الخاصة بالقوة 40 اللتي تظهر على شكل مثلث حينما نأخذ المومنت عند أي نقطة سواء نقطة A او B, لنفرض اننا نريد ان نأخذ المومنت عند النقطة B مع الإفتراض ايضا ان القوى اللتي تتحرك عكس عقارب الساعه بالنسبة للنقطة B تكون إشارتها موجبة, شاهد الصورة التالية:

لاحظ انه حينما تأخذ المومنت ويكون لديك قوى على شكل مثلث مثل القوى 40 فإنه لابد من تطبيق قاعدة خاصة وهي:

0.5 مضروبة في الإرتفاع او قوى المثلث وهي 40 مضروبة في قاعدة المثلث وهي مسافة المثلث من البداية الى النهاية وهي 2m, هذا كله عبارة عن قاعدة, مازلنا لم نضرب في المسافة بعد, والآن بعد تطبيق القاعدة ننتقل الى ضربها في المسافة, ولكن مسافة من بالضبط؟

الجواب: مسافة القوى 40 الى النقطة B اللتي اخذنا منها المومنت, جيد والآن ركز في الصورة اعلاه وانظر شكل المثلث الذي يبدأ من منتصف العارضة ومن ثم يكبر بشكل تدريجي الى ان يصل الى النقطة A  صحيح؟

جيد, والآن ركز في نهاية المثلث, بمعنى في آخر سهم يسقط فيه المثلث على العارضة وتحديدا عند النقطة A, يجب اولا أن تأخذ ثلث مسافة المثلث بحيث تكون قريبة من اخر سهم من المثلث الساقط على العارضة وتحديدا عند النقطة A, شاهد الصورة التالية:

لاحظ علامة الــ X ترمز الى انه اخذنا ثلث مسافة المثلث, ودائما تكون الثلث قريبة من اخر نقطة يسقط عليها المثلث, لاحظ اننا لم نضع علامة X في بداية المثلث مثلا وقلنا أن ثلث المسافة تبدأ من هناك, لا ولكن ثلث المسافة تبدأ على قرب من اخر سهم ساقط على العارضة من المثلث 

جيد والآن, نحن أخذنا المومنت في اي نقطة بالضبط؟

الجواب: نقطة B, وبالتالي سنتوجه الآن من علامة X الى النقطة B لأن هذه هي المسافة اللتي نريد إيجادها في حساباتنا, ولكن اولا علينا تحديد المسافة من علامة X الى بداية المثلث, هذه المسافة كما هو موضح بالصورة أعلاه بشكل مفصل تساوي 2/3 مضروبة في 2 , اولا قلنا 2/3 لأننا سنتوجه الى يمين المثلث, ركز عند علامة X سوف اسألك سؤالا, من خلال الجهة اليمنى من علامة X والجهة اليسرى, بالنسبة للجهة اليمنى اذا قمت بحساب المسافة من علامة X الى بداية المثلث هل هذه المسافة اكبر من المسافة اللتي اذا قمت بحسابها من علامة الــ X الى النقطة A؟

الجواب: نعم, لأن علامة X قريبة من A لأن ثلث المسافة يكون مركزا بقرب اخر سهم من المثلث او بقرب نهاية المثلث وبالتالي المسافة من علامة X الى النقطة A اقصر وبالتالي ستكون مسافتها 1/3 مضروبها في المسافة 2 بمعنى ثلث المسافة
ولكن حينما تحسب المسافة من علامة X الى بداية المثلث ستقول ثلثي المسافة مضروبة في مسافة المثلث, بمعنى 2/3 مضروبة في 2, وبالتالي طالما اننا نريد إيجاد مسافة القوى 40 من النقطة B, اذن يجب ان نحسب المسافة كاملة من النقطة B الى علامة X بمعنى سننتقل الى يمين X حتى نصل الى B, وبالتالي سنأخذ المسافة 2/3 مضروبه في 2 وهي المسافة مابين علامة X الى بداية المثلث كما هو موضح في الصورة أعلاه ومن ثم سنضيف عليها 2m وهي المسافة من بداية المثلث الى النقطة B

والآن لنفترض أننا نريد أن نأخذ المومنت عند النقطة A, كيف ستكون قيمة المسافة الخاصة بالقوى 40 إلى النقطة A؟, شاهد الصورة التالية:

لاحظ اولا علامة او إشارة السالب في بداية الحل, هذا بسبب اننا افترضنا ان القوى اللي تتحرك عكس عقارب الساعه تصبح قوى موجبة, وبما اننا أخذنا المومنت عند النقطة A ذلك يعني ان القوى تتحرك مع عقارب الساعه بالنسبة للنقطة A وبالتالي إشارتها سالبة, ومن ثم قمنا بتطبيق قاعدة المثلث بأخذ 0.5 ضرب القوى 40 ضرب مسافتها وهي 2, كما قلنا سابقا هذه قاعدة ومازلنا لم نضرب في المسافة, الآن سننتقل للمسافة, لاحظ هذه المرة اننا نريد أخذ المسافة من A الى علامة X اللتي شرحناها في الصورة السابقة, بمعنى اننا نريد حساب المسافة من علامة X الى النقطة A مما يعني اننا سنكتفي فقط بضرب القاعدة في 1/3 ضرب المسافة 2 كما هو موضح في الصورة أعلاه.