في هذه الصفحة سوف نقدم تمارين إضافية حول تحديد المعادلات التفاضلية من حيث كونها معادلات خطية ام لا, هنالك ثلاث نقاط أساسية لتحديد المعادلات الخطية من المعادلات التفاضلية تم شرحها بالتفصيل مع إضافة الأمثلة لكل نقطة في وقت سابق, بإمكانك مراجعتها في الرابط التالي:
https://assas2u.blogspot.com/2020/11/blog-post.html
دعونا نذكر النقاط الثلاث الأساسية واللتي ستكون كالآتي:
1- العناصر التابعة dependent variables ومشتقاتها "بمعنى درجات تفاضلها" يجب ان يكونوا جميعهم مرفوعين بالأس واحد"1"
2- يجب أن لاتكون العناصر التابعة dependent داخلة في أي شكل من أشكال الدوال
3- يجب ان لاتحتوي المعادلة التفاضلية على عناصر تابعة dependent ومشتقاتها بحيث تكون "مضروبة" في بعض
والآن لنبدأ بالمثال الأول, المطلوب هو تحديد المعادلة التفاضلية من حيث كونها معادلة خطية ام لا, شاهد الصورة التالية:
لكي نحدد إن كانت هذه المعادلة التفاضلية خطية ام لا, يجب أولا تحديد العنصر التابع والذي يطلق عليه dependent variable, ماهو هذا العنصر من خلال المثال الموجود في الصورة أعلاه؟
الجواب: y, لأن صيغة y ظهرت بصيغة تفاضلية من نوع Prime notation, لاحظ العلامة (") الموجودة على y مضروبة في (x) هذه الصيغة تسمى Prime notation, ومن هنا تستطيع التحديد ان العنصر الذي يكون خارج القوس هو العنصر التابع والذي يطلق عليه dependent variable, اما العنصر الموجود بين قوسين وهو X يسمى Independent variable
والآن من خلال النقاط الثلاث الأساسية اللتي أشرنا إليها في الأعلى سوف نقوم بتفصيل هذه المعادلة وتحديد ما اذا كانت معادلة خطية ام لا
أولا بالنسبة للنقطة الأساسية الأولى اللتي مفهومها هو ان جميع عناصر الــ dependent variable وهو y يجب ان يكونو مرفوعين بالأس 1, لاحظ ان العنصر y من الجهة اليسرى الذي فوقه علامة (")واللتي ترمز لدرجة الإشتقاق وهي الدرجة الثانية, نلاحظ انها مرفوعة بالأس 1 (تركيزك يكون بعناصر الــ dependent variable فقط), ولاحظ ايضا العنصر الثاني من y في المنتصف المضروب في الرقم 5 مرفوعة بالأس 1 (انتبه رقم 4 بين قوسين يرمز لدرجة الإشتقاق وليس لقيمة الأس), لاحظ ايضا بالنسبة للعنصر الآخر من y "مابعد إشارة =" المضروبة في Ln ايضا مرفوعة بالأس 1, وبالتالي النقطة الأولى الأساسية تحققت, ولكن هذا ليس كافي لتحديد المعادلة التفاضلية من حيث كونها خطية ام لا, حيث ان هنالك نقطتين آخرين بحاجة للتحقق منها, والآن لنتحقق من النقطة الثانية واللتي تنص على:
أن لاتكون العناصر التابعة dependent داخلة في أي شكل من أشكال الدوال
المقصود هنا ان لاتكون y داخلة في أي دالة, هل y من خلال المثال الموجود في الصورة أعلاه داخلة في دالة معينة؟
الجواب: نعم, لاحظ الدالة Lny, هي دالة Ln تحتوي على y, وطالما أن y من العناصر التابعه او dependent variable فلا يجب ان تكون داخلة في محتوى هذه الدالة او اي دالة اخرى (بمعنى لو كانت x موجودة في محتوى الدالة Ln واصبحت Lnx بدلا من Lny, هنا سوف نقول ان النقطة الثانية تحققت), ولكن هنا نتوقف ونقول ان النقطة الثانية لم تتحقق لأن y وهو العنصرdependent ظهرت في دالة معينة وهي Ln, وبالتالي هذه المعادلة التفاضلية هي معادلة غير خطية "Non Linear equation"
في المثال الثاني وكما هو واضح في الصورة أعلاه, ظهرت صيغة التفاضل هذه المرة بصيغة مختلفة عن المثال الأول, حيث أن صيغة التفاضل هذه هي من نوع Leibniz notation واللتي تظهر على شكل بسط ومقام, في هذه الصيغة التفاضلية لتحديد العنصر dependent كل ماعليك فعله هو التركيز في العنصر الموجود في البسط وهو العنصر L حيث انه موجود في البسط اما K موجودة في المقام, وبالتالي العنصر التابع او المعرف بــ dependent سيكون العنصر L
والآن لنتحقق من النقطة الأساسية الأولى واللتي مفهومها أن جميع عناصر الــ dependent يجب ان يكونو مرفوعين بالأس 1, نلاحظ من الجهة اليسرى أن الرقم 3 ترمز لدرجة الإشتقاق ولا ترمز لقيمة الأس, قيمة الأس هنا تساوي 1, ولاحظ ايضا بالنسبة لــ L الموجودة في المنتصف بصيغة dL/dk حيث ان قيمة الأس هنا ايضا تساوي 1, لكن لاحظ في العنصر الثالث من L واللتي ظهرت في صيغة دالة وهي SinL , نلاحظ هنا ان L داخلة في دالة Sine ولكن قد يكون هذا مقبول في النقطة الأولى الأساسية لتحديد المعادلات الخطية من المعادلات التفاضلية, ولكن بالنسبة للنقطة الثانية فــ هنا نتوقف ونقول ان ذلك غير متوافق لماذا
الجواب: لأن L عنصر من عناصر الــ dependent وبناءً على النقطة الأساسية الثانية, يجب أن لا تكون L داخلة في أي شكل من أشكال الدوال, وبما أنها داخلة في دالة Sine, اذن هنا نتوقف ونقول أن هذه المعادلة التفاضلية هي معادلة غير خطية


مثال آخر, وكما نلاحظ في الصورة أعلاه ان الصيغة التفاضلية اللتي ظهرت في هذا المثال هي من نوع Leibniz notation واللتي تظهر على شكل بسط ومقام, وكما شرحنا في المثال السابق, لتحديد العنصر dependent من هذه الصيغة كل ماعليك فعله هو التركيز في العنصر الموجود في البسط, كما نلاحظ ان العنصر المتواجد في البسط هو العنصر X, وبالتالي هو العنصر dependent الذي سوف نركز عليه, والآن بناءً على النقطة الأساسية الأولى واللتي تنص على ان جميع عناصر dependent يجب ان يكونو مرفوعين بالأس 1, نلاحظ بدايةً من الجهة اليسرى ان قيمة الأس بالنسبة للعنصر x يساوي 1, وبالنسبة للعنصر الآخر من X "مابعد إشارة الزائد" ايضا قيمة الأس تساوي 1, اذن هنا نقول النقطة الأساسية الأولى تحققت, اما بالنسبة للنقطة الأساسية الثانية واللتي تنص على انه يجب أن لاتكون العناصر التابعة dependent داخلة في أي شكل من أشكال الدوال, نلاحظ أن X ليست داخلة في شكل من أشكال الدوال, اذن النقطة الثانية تحققت, والآن لنتحقق من النقطة الثالثة الأساسية واللتي تنص على انه يجب ان لاتحتوي المعادلة التفاضلية على عناصر تابعة dependent ومشتقاتها بحيث تكون "مضروبة" في بعض, بمعنى ضروري جدا ان عناصر X بحكم انها عناصر dependent يجب ان لاتكون مضروبة في بعض, نلاحظ من الجهة اليسرى أن y مضروبة في dx/dy, هنا ليست مشكلة لأن النقطة الثالثة تتحدث عن عناصر الــ dependent وهي x, وبالتالي y حتى وان كانت مضروبة في dx/dy فهي لاتؤثر
اذن تم التحقق من النقطة الثالثة الأساسية وهي متوافقة مع هذه المعادلة, وبالتالي تحققنا من جميع النقاط الثلاث الأساسية, اذن هذه المعادلة التفاضلية هي معادلة خطية "Linear in X"
Leibniz notation واللتي دائما ما تكون على شكل بسط ومقام, وبالتالي تركيزك سيكون على العنصر الموجود في البسط وهو العنصر f, وبالتالي f هو العنصر dependent, والآن لنتحقق من النقطة الأساسية الأولى , هل جميع عناصر dependent مرفوعة بالأس 1؟
الجواب: نعم, حيث ان الأرقام 4 و 2 هي مجرد ارقام ترمز لدرجة الإشتقاق وليس لقيمة الأس, قيم الأس جميعها تساوي 1, اذن النقطة الأولى الأساسية تحققت
والآن لنتحقق من النقطة الثانية, هل العنصر f داخل في اي شكل من اشكال الدوال؟
الجواب: لا, لايوجد في المعادلة دالة معينة, وبالتالي النقطة الثانية تحققت
ماذا عن الثالثة؟ واللتي تنص على انه يجب ان لاتكون عناصر dependent مضروبة في بعض
الجواب: لم تتحقق, لاحظ أن f مضروبة في d2f/dx2, بمعنى ان f مضروبة في العنصر df الموجود في البسط وكلاهما عناصر dependent, وبالتالي النقطة الثالثة الأساسية لم تحقق, اذن هذه المعادلة التفاضلية هي معادلة غير خطية"Non Linear equation"

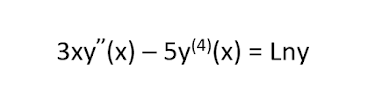




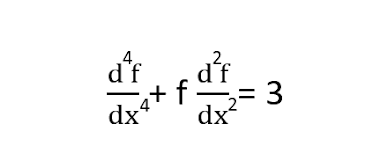


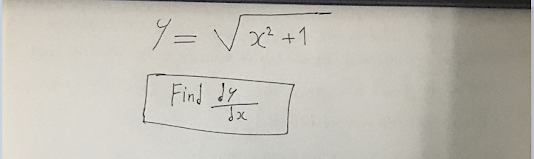

تعليقات
إرسال تعليق