المطلوب من خلال هذا التمرين هو إيجاد الحل العام للمعادلة التفاضلية الخطية بصيغة الحل الصريح او ما يعرف بالإنجليزية
Explicit solution
والمقصود بهذه الصيغة هي بجعل العنصر y وحيدا في جهة مستقلة من المعادلة مرفوعة بالأس واحد ان امكن لتصبح بالصيغة المطلوبة Explicit
غير ذلك تسمى صيغة الحل بــ Implicit solution
وهي تعتبر الخطوة الخامسة من الحل او آخر خطوات حل هذا التمرين
هيا بنا لنبدأ بأولى خطوات الحل:

الخطوة الأولى:
- التأكد فيما اذا كانت المعادلة التفاضلية المعطاة لك في التمرين مطابقة للقاعدة الأساسية ام لا
نلاحظ ان المعادلة التفاضلية المعطاة مطابقة للقاعدة الأساسية, حيث أن كل العناصر متوفرة ولا يوجد عنصر زائد في المعادلة مما يستوجب عمل بعض العمليات لتحقيق التوافق او مطابقة القاعدة الأساسية
اذن المعادلة التفاضلية المعطاة مطابقة للقاعدة الأساسية
الخطوة الثانية:
- إيجاد قيمة Mx
والمقصود بــ Mx هو إيجاد الناتج النهائي من الدالة e مرفوعة بتكامل الأس Px
(لاحظ ان التكامل يختص فقط بالأس Px الخاص بالدالة e )
الناتج النهائي من هذا التكامل مع الدالة e تكون هي قيمة Mx
الخطوة الثالثة:
- قم بضرب القيمة Mx اللتي اوجدتها في الخطوة الثانية في كل خانة من المعادلة كما هو موضح لك في الصورة أعلاه
الخطوة الرابعة:
- دائما تجاهل الخانة الأولى من المعادلة وفقا لآلية خطوات الحل, ومن ثم اوجد التكامل والتفاضل بنفس الوقت للخانة الثانية, ثم بعد ذلك اوجد التكامل فقط للخانة الثالثة من المعادلة
توضيح: الناتج من عملية التكامل والتفاضل بالنسبة للخانة الثانية تساوي نفس القيمة دائما من دون اي تغيير كما تلاحظ في الصورة أعلاه
اما الناتج من تكامل الخانة الثالثة من المعادلة سيكون ناتج تكامل عادي, بحيث تجري عملية تكامل عادية للدالة
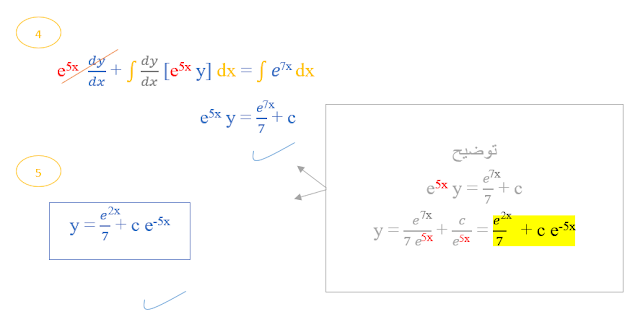
الخطوة الخامسة والأخيرة:
- تحويل الحل الذي تحصلت عليه في الخطوة الرابعة الى صيغة الحل الصريح او مايعرف بالإنجليزية Explicit solution
وهو بجعل العنصر y وحيدا في جهة مستقلة مرفوعة بالأس 1 ونقل المعاملات له للجهة الاخرى من المعادلة
وبالتالي تصبح هذه الإجابة هي الإجابة النهائية لهذا التمرين
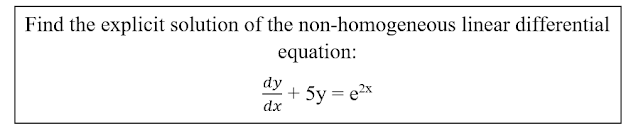






تعليقات
إرسال تعليق